Decision Tree & Random Forest

Decision Tree

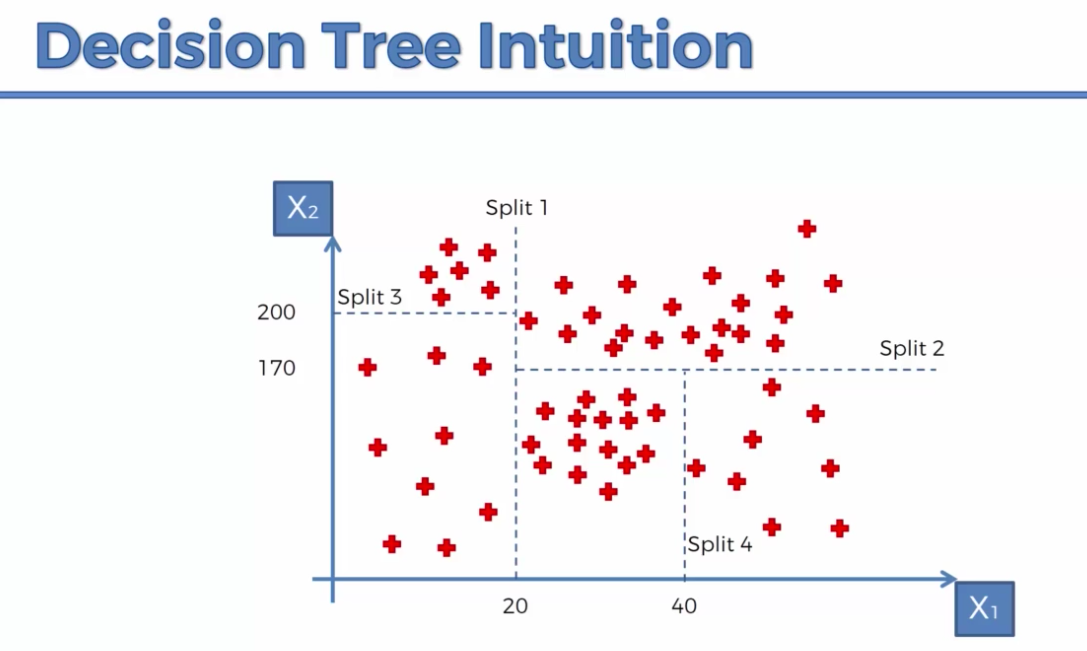
How it works

each split part is called a "leaf"
the splitting uses information entropy

How to choose what features to split on each node?

maximize purity, reduce entropy

When do you stop splitting?

when a node is a 100% one class (entropy = 0)

before the tree exceeds max depth

when improvement in purity is below a threshold score (i.e. reduced entropy/information gain)

when the sample number in a new node is below a threshold number

Steps

choose one feature and find the best split of this feature
repeat Step 1 for other features (brute force)
select the feature with the split that leads to purest labels/max information gain
repeat from root node to leaf nodes till data is pure

Pruning a decision tree

Pruning consists of going back through the tree once it’s been created and removing branches that don’t contribute significantly enough to the error reduction by replacing them with leaf nodes.
It is a bottom-up technique that solved overfitting.
Two approaches:
- pre-pruning: prune while growing the tree
- post-pruning: start pruning once the tree is built to its depth

Hyperparameters

max depth of the tree

Pros & Cons

Pros

can generate feature importance
very fast: efficient in training and prediction

Cons

overfitting
sensitive to outliers

Metrics

Information gain
- = the reduction of uncertainty given some feature
- it is also a deciding factor for which attribute should be selected as a decision node or root node
Gini impurity (or Gini index)
- = likelihood of some data being misclassified when selected randomly
- varies between values 0 and 1,
  - 0 indicates the purity of classification, i.e. all the elements belong to a specified class or only one class exists there.
  - 1 indicates the random distribution of elements across various classes
  - 0.5 indicates an equal distribution of elements over some classes

Random Forest

Random forest is a Ensemble Learning method as an ensemble of Decision trees, which is necessary, because a single tree is sensitive to small changes of the data.

How it works

pick at random K data points from the training set, with bootstrapping
build the decision tree associated to these K data points. At each node:

randomly select $d$ features without replacement
split the node using the feature that provides the best split that leads to purest labels/max information gain

If $n$ features are available:

for classification, the default is $d = \sqrt{n}$

for regression, the default is $d = n / 3$

repeat Steps 1&2 according to the number of trees you prefer (usually > 500 tress)
predicted value = average of predicted values across all trees

Hyperparamters

number of trees
less commonly used in practice:
- bootstrap sample size $K$ in Step 1
- number of features $d$ in Step 2